2020-2021学年度高中数学期中考试卷

试卷副标题

第I卷（选择题）

【题型】一、单选题

【题干】

1、设集合，，则（ ）

A．                                        B．

C．                                           D．

【知识点】集合的概念及运算

【难度】

【答案】C

【解析】

[分析]根据集合交集运算求解即可得答案.

[详解]

解：

故选：C

【题干】

2、设，命题“存在，使方程有实根”的否定是（ ）

A．对，方程无实根 B．对，方程有实根

C．对，方程无实根 D．对，方程有实根

【知识点】特称命题的否定及其真假

【难度】

【答案】A

【解析】

[分析]

只需将“存在”改成“任意”，有实根改成无实根即可.

[详解]

由特称命题的否定是全称命题，知“存在，使方程有实根”的否定是

对，方程无实根

故选：A

第II卷（非选择题）

【题型】二、填空题

【题干】

5、已知函数，则______．

【知识点】

【难度】

【答案】

【解析】

[分析]

先对函数求导，然后代值计算即可

[详解]

解：由，得，

所以，

故答案为：2021

【题干】

6、设，满足约束条件，则的最小值为___________.

【知识点】

【难度】

【答案】

【解析】

[分析]

作出可行域，作出目标函数对应的直线，平移该直线可得最优解．

[详解]

解：作出可行域，如图阴影部分，作直线，由得，知直线向上平移时，减小，平移直线，如图所示，它过时取得最小值，的最小值是.

故答案为：．

【题干】

7、某歌手电视大奖赛中，七位评委对某选手打出如下分数：，则其百分位数为________．

【知识点】

【难度】

【答案】

【解析】

[分析]

由题意，数据按照从小到大的顺序排列，分析得百分位数即为这组数据的中位数，所以找第个数据.

[详解]

由题意可知，共有个数据并且已经按照从小到大的顺序排列，其百分位数即为这组数据的中位数，所以其百分位数是第个数据为.

故答案为：

【题型】三、解答题

【题干】

10、某环保组织进行了关于生态文明建设的知识竞赛，随机调查了人，并统计了这人答对的题数，将统计数据分为，，，，，六个小组，得到频率分布直方图如图所示．已知答对题数在，，三组内对应的人数依次成等差数列．

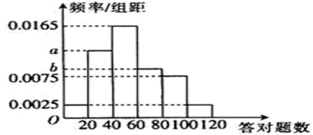
（1）求频率分布直方图中，，并估计这人答对题数的中位数（精确到整数位）；

（2）若答对题数属于记为不合格，属于记为优秀，现在要从不合格和优秀的人中用分层抽样的方法抽取人，再从这人中随机抽取人．求至少有人为优秀的概率．

【知识点】

【难度】

【答案】（1），，52；（2）.

【解析】

[分析]

（1）由，，三组内对应的人数依次成等差数列，可得这三组对应的频率成等差数列，从而可得，再由各组的频率和为1，列方程组可求出，，由于前2组的频率和小于，前3组的频率和大于，所以可知中位数在第3组，从而可求出中位数；

（2）由分层抽样先计算出不合格的人数和优秀的人数，再利用列举法求概率

[详解]

解：（1）由题意得，解得，

又，．

，所以中位数大约是．

（2）不合格的人数为：，

优秀的人数为：，

所以“优秀”抽取人，

“不合格”抽取人，

设两名“优秀”的人记为：，，三名“不合格”的人记为：，，，

则这人中任选人有：，，，，，，，，，共种情形，至少有人为优秀有：

，，，，，，，共有7种，

因此至少有人为优秀的概率为．